2.2 数项级数的基本概念
一、数项级数的定义及敛散性
注意:级数一定是由无穷多项相加而成的式子. 例如: |
|
由中学学过的无穷递缩等比数列的求和公式可得 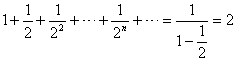 , ,而对于级数 接下来要研究的问题是:“无穷项求和”的运算如何进行?
|
|
典型例题 例 2.2.1 讨论等比级数(又称为几何级数) 解 (1)如果 当 (2)如果 |
|
综上所述,我们得到:等比级数
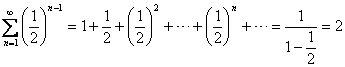 ,级数收敛. ,级数收敛.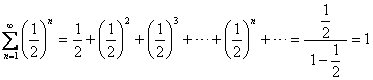 ,级数收敛. ,级数收敛. |
|
例 2.2.2 判定下列级数的敛散性: (1) 解 (1)∵ ∴ 从而 (2)由于 |
|
例 2.2.3 判定级数 解 级数的前 因为 也可以这样化简 备注:这里用到初等数学中的公式: |
二、级数的基本性质和收敛的必要条件性质1 若 性质2 设级数 |
|
性质3 在级数中去掉、加上或改变前面有限项的值,不会改变级数的敛散性. 性质4(级数收敛的必要条件) 若级数 推论:若 注意:级数的一般项趋于零并不是级数收敛的充分条件.有些级数虽然一般项趋于零,但仍然是发散的.将在后面学习的调和级数就是这样的例子. |
|
典型例题 例 2.2.4 判断级数 解 例 2.2.5 判定级数 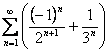 的敛散性,若收敛求此级数的和. 的敛散性,若收敛求此级数的和.解 因为级数 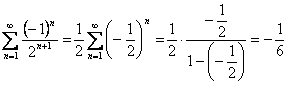 , , ;所以由性质2, ;所以由性质2,
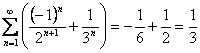 . . |
|
例 2.2.6 判定级数 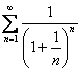 的敛散性. 的敛散性.解 级数的一般项为 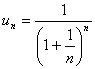 ,因为 ,因为
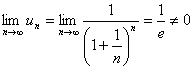 , , |
三、正项级数的敛散性判别
有了这个定理,在判断一个正项级数的敛散性时,可以利用另一个收敛性为已知的正项级数来比较. 形如 |
|
典型例题 例 2.2.7 判定下列级数的敛散性: (1) 解 (1)因为 (2)因为 (3)因为 |
|
例 2.2.8 判定下列级数的敛散性: (1) 解 (1) ∵ (2) ∵ ∴ (3) ∵ |
|
请认真答题,测试一下你对前面知识点的学习情况!
4.(单选题)![]() =( )
=( )
【答案】D
【解析】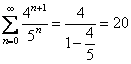
【知识点】等比级数