2.4 无穷小量和无穷大量
一、无穷小量1、 无穷小量的概念
例如,因为 因为 因为 因为 注意: (1)无穷小量是指极限为零的量,不是指“很小的数”,所以 (2)无穷小量与自变量的变化趋势相关联,例如, |
|
2 、 无穷小量与函数极限的关系
这个定理阐述了无穷小与函数极限的关系:设在自变量 |
|
3 、无穷小量的性质 (1)有限个无穷小的代数和是无穷小. (2)有限个无穷小的乘积是无穷小. |
|
(3)有界函数与无穷小的乘积是无穷小. (4)常数与无穷小之积是无穷小. 典型例题 例 2.4.1 求下列极限: (1) (3) 解 (1) ∵ ∵ 故 (2) ∵ 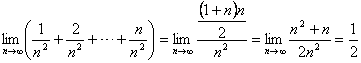 . . |
二、无穷大量1 、无穷大量的概念
这里的极限也可以只考虑单侧. 例如: 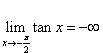 ,∴ ,∴ |
|
注意: (1)无穷大是指绝对值无限变大的量,不是指“很大的数”,所以 (2)无穷大与自变量的变化趋势相关联,例如, |
|
2 、无穷小与无穷大的关系
例2.3.9中求极限 ∵ 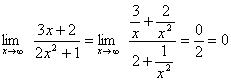 ,∴ ,∴ |
|
典型例题 例 2.4.2 判断下列函数在指定的过程中是无穷大量还是无穷小量. (1) (3) 解 (1)因为 (2)因为 (3)因为 (4)因为 |
三、无穷小量的比较无穷小是极限为零的变量,但在无限接近零的过程中,还有个接近的快慢程度问题. 请看下表,这里列出了函数
|
对于(1)的情形,可以这样理解. |
|
注意 只有同一个变化过程中的 无穷小,才可以进行比较. 例如,当 在例2.3.11中曾求出极限 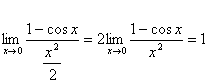 , ,所以, |
|
典型例题 例 2.4.3 证明 当 证 (1)因为 所以 (2)求 |
四、等价无穷小在求极限中的应用可以证明,求极限时,分子或分母中 的无穷小乘积因子可用其等价无穷小代换.这种代换常使极限计算简化. 最常用的等价无穷小有:当 |
|
典型例题 例2.4.4 求下列极限: (1) (3) 解 (1) (2) (3) 原式= 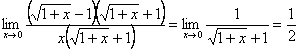 . .或者利用 原式= 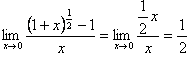 . .(4) 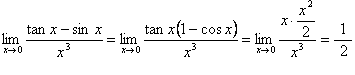 .( .(注意 求极限时,分子或分母中的无穷小乘积因式可用其等价无穷小代换,但加减运算中的各项不能作等价无穷小代换.例如,以下做法是错误的: |
|
例 2.4.5 当 (A) 解答>>
|
|
请认真答题,测试一下你对前面知识点的学习情况!
6.(单选题)![]() ( ).
( ).
【答案】A
【解析】![]()
【知识点】有界函数与无穷小的乘积是无穷小