5.2 不定积分的换元法
前言本节介绍不定积分的换元法.换元法通常分成两类:第一类换元法和第二类换元法. |
一、第一类换元法(凑微分法)
举一个公式为例.因为 |
|
例:若 又如,若 注意到 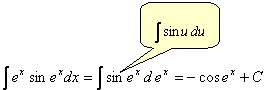
这就是第一类换元积分法,也就是所谓的凑微分法. |
|
典型例题 例5.2.1 求 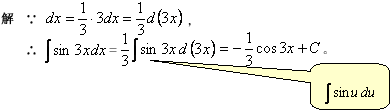
例5.2.2 求 分析 因为 解 例5.2.3 求 解 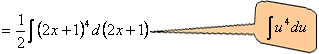
|
|
例5.2.4 求下列不定积分 (1) 解 (1) = (2) 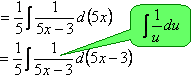
(3) = = (4) 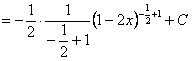
|
|
课堂练习1 求下列不定积分: (1) (2) (3) (4) (5)
|
|
常用的凑微分公式
例5.2.5 求不定积分 解 = = = 例5.2.6 求 解 例5.2.7 设 解 由题设, 于是, |
|
例5.2.8 求下列不定积分:(本例结果作为公式记忆) (1) (2) (3) (4)
|
|
补充公式(9个)
|
二、第一类换元法(凑微分法)(续)首先请同学们默记下列常用的凑微分公式: |
|
典型例题 例5.2.9 设 解 例5.2.10 求下列不定积分 (1) (2) (3) (4) 解 (1) (2) 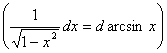
(3) (4) = 方法2 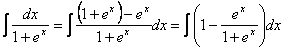
可以推出: |
|
例5.2.11 求下列不定积分 (1) (2) 解 (1) (2) |
|
例5.2.12 求不定积分 解 = = = 类似地可以得到公式: |
|
例5.2.13 求下列不定积分 (1) 解: (1)前面有道例题是 = = = (2) = = = (3) = = = (4) = = |
|
|
例5.2.14 计算下列积分: (1) 解: (1) 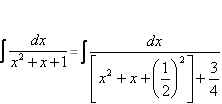
= 
= 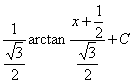
= (2) = = = = = (3) 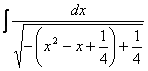
= 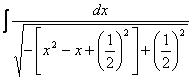
= 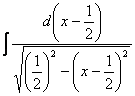
= 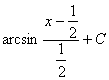
= 方法2 = 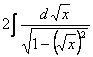
= |
|
例5.2.15 求 解 = =
例5.2.16 求不定积分 解 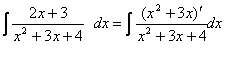
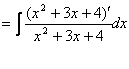
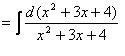
|
三、第二类换元法
说明: (1) 第二换元法主要用于去掉被积函数中的根号; (2) 被积函数含有根号时,可考虑用第二换元法,但有时并非必用不可. (3) 被积函数不含根号时,有时也可用第二换元法,作变量代换,引入新变量来简化运算. |
|
典型例题 例5.2.17 求下列不定积分: (1) 解 (1) 令 = = = = (2) 令 = = = =
|
|
例5.2.18 求 分析 如果令 解 利用三角恒等式 于是 = = = = = 由于  = =于是 = 注:" 后面的例5.2.19和例5.2.20中,求不定积分 |
|
例5.2.19 求 解 利用三角恒等式 于是 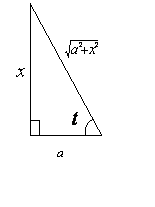 作右图所示的直角三角形,辅助分析,可得: 作右图所示的直角三角形,辅助分析,可得:于是 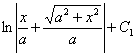
= 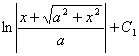 = =其中 例5.2.20 求 解 利用三角恒等式 令 于是 = 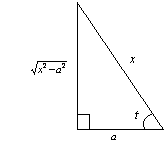 作右图所示的直角三角形,辅助分析,可得: 作右图所示的直角三角形,辅助分析,可得:于是 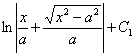
= 其中
|
|
例5.2.21 求下列积分: (1) 解 (1) (2) = (3) 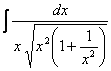 = =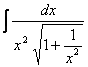 = 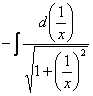 = 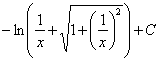 (公式 (公式= (4) = = |
|
例5.2.22 求解不定积分 解 方法1 = 方法2 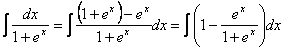
方法3 令 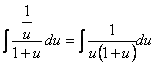
= = |
|
例5.2.23 计算下列不定积分: (1) (2) 解 (1) 令 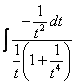
= = = = 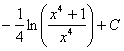
= (2) 令 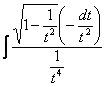
= = = = 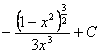 . .本例中所用的方法称为倒代换. |
请认真答题,测试一下你对前面知识点的学习情况!
17.![]() ( )
( )
【答案】A
【解析】![]()
【知识点】第一类换元法
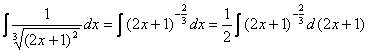

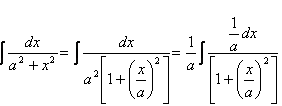
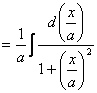
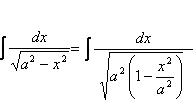
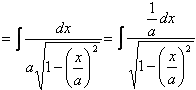
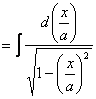 (运用基本公式
(运用基本公式 一般地,计算
一般地,计算 计算
计算 当被积函数为有理假分式时,先将其转化为多项式与真分式的代数和.
当被积函数为有理假分式时,先将其转化为多项式与真分式的代数和. 若分子恰是分母的导数,则
若分子恰是分母的导数,则