5.3 分部积分法

　　熟悉常用的凑微分公式对于学好本节课的内容是十分必要的，请背记一遍再进入新课的学习．

　　常用的凑微分公式： 　　
　　
　　
　　  

　　分部积分法
　　，，两边求不定积分，得
　　　　　　　　　　　　，
　　即
　　　　　　　　　　　　．
　　上述公式称为分部积分公式．
　　公式的结构如图：
　　　　　　　　　　　　


　　典型例题
　　例5.3.1　求．
　　解　＝　
　　　　　　　　 ．
　　若换一种凑微分的方式：
　　　　　　　　　　　　　　　　　　　　　　　＝
　　上式右端的积分比原积分更难求出．由此可见，在利用分部积分法时，适当选取和是非常关键的．
　　选取和的两个原则：
　　（1）　较容易凑出；
　　（2）　要比容易求出．

　　例5.3.2　求．
　　解　=
　　　　　　　　　＝
             　　=．
　　例5.5.3　计算．
　　解　=
             　　　=
             　　　=
             　　　=
             　　　=
                 　=．
如果被积函数是幂函数与三角函数或幂函数和指数函数的乘积，就可以考虑用分部积分法计算，并且令幂函数为．这样，每用一次分部积分公式就可以使幂函数的幂降低一次，从而化简积分．这里假定幂指数是正整数．

　　课堂练习1
　　（1）　
　　（2）　
　　（3）　
　　      
　　解：
　　（1）　＝
　　（2）　＝
　　　　　　　　　　＝
　　　　　　　　　　＝
　　　　　　　　　　＝＝
　　　　　　　　　　＝．
　　（3）　＝
　　　　　　　　　　　　＝
　　　　　　　　　　　　＝．
　　你做对了吗
　

　　例5.3.4　求不定积分．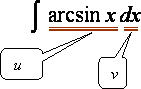
　　解　=
             　　　=
　　　　　　　　　　＝　　（）
          　 　　　=
　　　　　　　　　　=　　（）
           　　　　=．

　　例5.3.5　求．
　　解　=
               　　　=
               　　　=　　
               　　　=
               　　　=
               　　　=．
　　如果上例中考虑到的导数是，第一步就凑微分为：
　　　　　　　　　　=，
　　继续往下求解就方便多了．

　　典型例题
　　例5.3.6　求．
　　解　=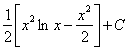
            　　=
            　　=
            　　=
            　　=．
如果被积函数是幂函数与反三角函数乘积或幂函数与对数函数的乘积，就可以考虑用分部积分法求不定积分，并且令反三角函数或对数函数为．

　　例5.3.7　计算．
　　解　=
             　　　=
             　　　=
             　　　=
             　　　=
             　　　=
             　　　=，
　　移项，得
                 　　 =　
　　从而
                     =，
　　其中．
如果被积函数是指数函数和正弦（或余弦）函数的乘积，考虑用分部积分法．经过两次分部积分后会出现原来的积分，通过合并同类项即可求得不定积分．

　　说明：若第一次分部积分时是用指数函数和去凑微分，第二次分部积分时仍需用指数函数和去凑微分；如果第一次是用三角函数和去凑微分，那么第二次也得用三角函数和去凑微分．

　　例5.3.8　计算不定积分．
　　解　令，则，，于是
　　　　　=＝
             　　　=
             　　　=
             　　　=
　　　　　　　　　　＝．

　　例5.3.9　设有一个原函数为，求．
　　解　由题设，有一个原函数为，因此的全体原函数
　　　　　　　　　　　　　＝，
　　且=＝．
　　从而
　　　　　　　　　　　　　＝
　　　　　　　　　　　　　　　　　　＝．
　　　　　　　　　　　　　　　　　　＝　（）
　　　　　　　　　　　　　　　　　　＝．
　　如果由=，再求导得，最后代入加以计算，则会增加计算量．