5.6 定积分的基本性质
复习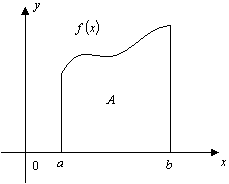
为了以后计算及应用方便,我们对定积分作以下两点补充规定: 补充规定: 1、 2、 |
定积分的性质性质1 性质2 性质3 这条性质也叫定积分对于积分区间具有可加性. 
性质4 若在积分区间 从几何上看, 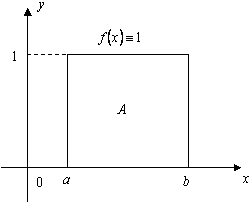
|
|
性质5 若在区间 从几何上看,当 
从几何上看,如下图所示,曲顶高的曲边梯形的面积大. 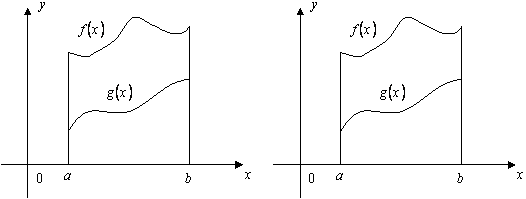
|
∴
|
|
典型例题 例5.6.1 设函数 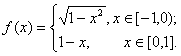
解 由性质3,定积分对于积分区间具有可加性 ∴ 由定积分的几何意义知, 
故 |
|
例5.6.2 试比较下列定积分的大小: (1) (2) 解: (1) 因为 |
|
例5.6.3 试估计下列定积分的值: (1) (2) 解: (1)∵在区间 ∴ |