5.7 定积分的基本公式(牛顿-莱布尼兹公式)
一、定积分的基本公式(牛顿-莱布尼兹公式)
|
|
典型例题 例5.7.1 求定积分 解 因为 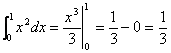 . .解 因为 所以 
|
|
例5.7.3 求 解 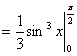
|
|
典型例题 例5.7.4 求 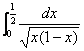 . .解 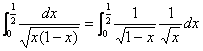 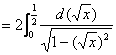  的形式 的形式
|
|
例5.7.5 (1) 求 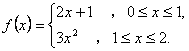
(2) 求 解: (1)被积函数 (2)这里被积函数中出现了绝对值,首先需化去被积函数的绝对值.与 同理,可得: 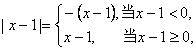
即 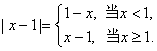
可见,被积函数 于是 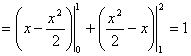 . . |
二、变上限的定积分变上限的定积分: 说明: (1) 变上限的定积分 例如,  ,可见,这是关于 ,可见,这是关于(2) 变上限的定积分 例如, 可见,当积分上限是 (3) 当积分上限是 = (4) 因为定积分的值与积分变量无关,所以 |
|
典型例题 例5.7.6 计算下列函数的导数: (1) (2) (3) 解: (1) (2) (3) |
|
例5.7.7 计算极限 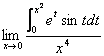 . .解 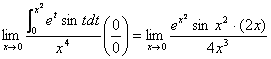
|
|
例5.7.8 求函数 解 当 (或者由 |
请认真答题,测试一下你对前面知识点的学习情况!
20. ( )
( )
【答案】B
【解析】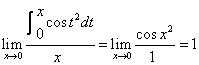
【知识点】变上限积分