5.10 定积分的应用
一、微元法复习: 设曲边梯形如图所示,则此曲边梯形的面积 |
|
第一步:取面积元素.如图所示,取 接着,作一个与窄曲边梯形同底的窄矩形. 窄矩形的底边长为 |
|
第二步:对面积元素在区间 简单地说,微元法就是在求区间 |
二、求平面图形的面积1、如图所示,设平面图形由曲线 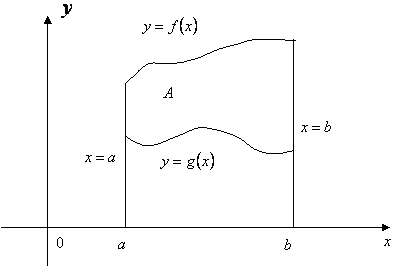
如动画所示,曲线 注意:需将被积函数表示为 |
|
也可用微元法分析,如图: 窄矩形的底边长为 特别地: (1) 平面图形如图所示,由曲线 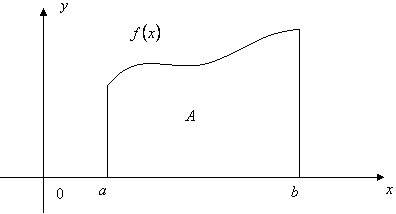
|
|
(2) 平面图形如图所示,由曲线 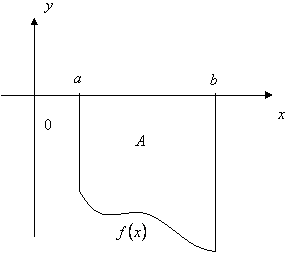
|
|
2、设平面图形由 注意:需将被积函数表示为 |
|
典型例题 例5.10.1 求由抛物线 解 
 或 或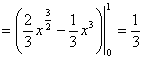
或者,也可选取 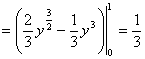 . . |
|
例5.10.2 求由曲线 解 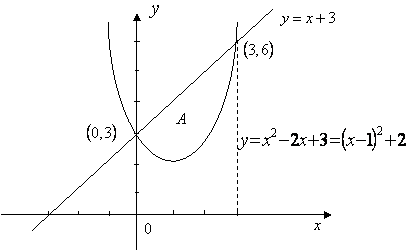
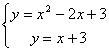 ,求得交点为 ,求得交点为
|
|
例5.10.3 求椭圆  解 由对称性,椭圆面积是其在第一象限部分的面积的4倍.因此,椭圆面积 解 由对称性,椭圆面积是其在第一象限部分的面积的4倍.因此,椭圆面积= |
三、求旋转体的体积旋转体就是一个平面图形绕其平面内的一条直线旋转一周而成的立体. 请想象:下列图形绕竖轴旋转后会成为什么样的立体? (1) 如图所示的矩形. (2) 如图所示的三角形. (3) 如图所示的直角梯形. |
|
用微元法来导出求旋转体体积的公式. 1、求连续曲线 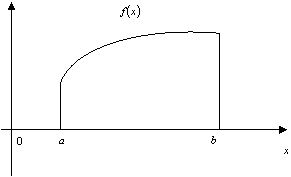
(见同济大学《高等数学》第四版,P.344图6-9) 如图所示,在区间 体积微元(元素): 旋转体的体积: 注意:平面图形绕 |
|
2、求连续曲线 体积元素: 旋转体的体积: 注意:平面图形绕 |
|
典型例题 例5.10.4 直线 解 直线 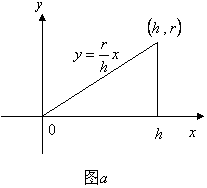
(见同济大学《高等数学》第四版,P.345图6-10) 体积元素为 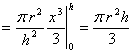
|
|
例5.10.5 计算由椭圆 解 这个旋转椭球体也可以看作是由上半椭圆 体积元素为 = 
|
四、求平面曲线的弧长设光滑曲线弧L在直角坐标系里的方程为 用微元法可分析得弧长的元素(弧微分):  , , |
|
典型例题 例5.10.6 计算曲线 解 因为 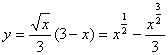 , ,所以 
|
|
例5.10.7 证明半径为 解 以圆心为原点建立坐标系.则圆的方程为 由对称性,圆的周长等于其位于第一象限部分的弧长的4倍. 方法1 位于第一象限内的圆弧的方程为 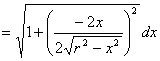
因此圆周的长度为 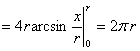
|
五、定积分在物理上的应用1、变速直线运动的位移 设物体作变速直线运动,其速度为 在 2、变力沿直线所作的功 设物体在变力 在 |
|
典型例题 例5.10.8 已知上抛物体的运动速度为 解 由变速直线运动的位移公式,得所求位移为 |
|
例5.10.9 根据虎克定律,弹簧的弹力与形变的长度成正比.已知汽车车厢下的减震弹簧压缩1cm需力14000N,求弹簧压缩2cm时所作的功. 解 由虎克定律,弹簧的弹力为 由题设, 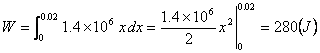
|
请认真答题,测试一下你对前面知识点的学习情况!
22.由曲线xy=1与直线y=2,x=3所围成的平面图形的面积是( )
【答案】A
【解析】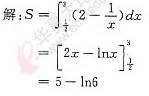
【知识点】求平面图形的面积
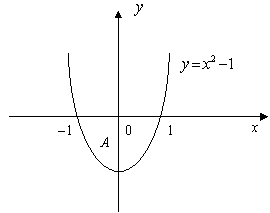
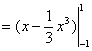
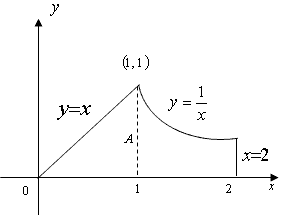
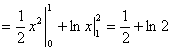
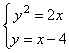

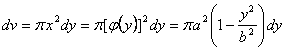 ,
,