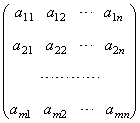6.3 矩阵的概念及矩阵的初等行变换
一、矩阵的概念现实生活中我们常常会看到用表格来描述事物.例如,某厂向三个商店发送四种产品的数量可列成下面这样的表格. 其中 这是一个3行4列的数表. 又如,三元线性方程组 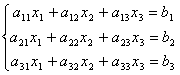 , ,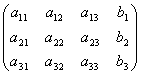
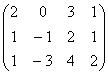
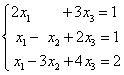 , , |
|
1、矩阵的定义
说明: 1. 矩阵和行列式不是一个概念,行列式是方的,运算结果是一个数,而矩阵只是个数表,且行数和列数可以不一致. 2. 对于线性方程组,由其系数和常数项构成的可用于抽象地表示该方程组的矩阵称为该方程组的增广矩阵. 例如,二元线性方程组 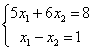 的增广矩阵为 的增广矩阵为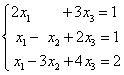 的增广矩阵为 的增广矩阵为
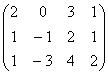 . . |
|
2、 几种特殊的矩阵 (1)方阵:当矩阵 例如,三阶方阵 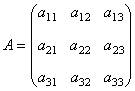 的行列式是 的行列式是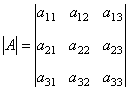 . .(2)行矩阵和列矩阵:只有一行的矩阵称为行矩阵;只有一列的矩阵称为列矩阵. (3)零矩阵:所有元素都为0的矩阵称为零矩阵. 问:下列两个矩阵相等吗? 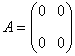 , ,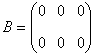
(4)上三角矩阵、下三角矩阵、对角阵与单位阵 主对角线上的元素称为主对角线元素. 如果方阵主对角线的下方元素全为零,称之为上三角矩阵. 如果方阵主对角线的上方元素全为零,称之为下三角矩阵. 如果方阵除对角线以外,所有元素全为零,称之为对角阵,可用记号dig表示. 如果方阵主对角线元素全为1,而其余元素全为零,则称之为单位阵,记为 |
二、矩阵的初等行变换1、 矩阵初等行变换的定义
当矩阵 注意:矩阵的初等行变换在表述形式上与行列式相应的运算类似,但从本质上说,两者是完全不同的. 例如:对矩阵 |
|
2、 行阶梯形矩阵和行最简矩阵 (1) 行阶梯形矩阵 
(2) 行最简矩阵 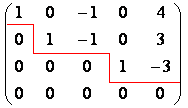
可以证明:任何一个矩阵均可以通过初等行变换变成一个行阶梯形矩阵,并进一步变成行最简矩阵. |
|
典型例题 例6.3.1 利用初等行变换将矩阵 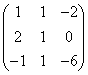 化为行最简矩阵. 提示>> 化为行最简矩阵. 提示>>
解 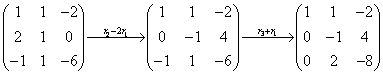
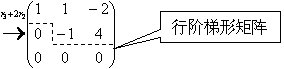 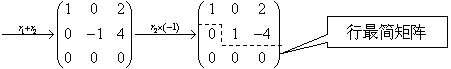
|
|
例6.3.2 设三元线性方程组为 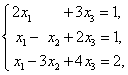
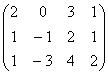 , ,解 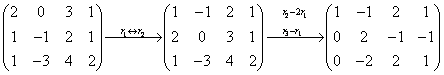
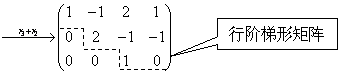
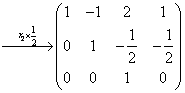 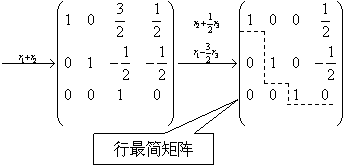
|
|
课堂练习 对矩阵 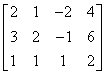
矩阵 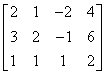 的行最简形是 的行最简形是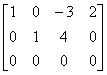 ,你做对了吗?如果不对请检查一下问题出在哪里. ,你做对了吗?如果不对请检查一下问题出在哪里. |