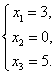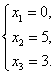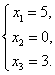6.4 解线性方程组的消元法
复习1、线性方程组可以用它的增广矩阵来描述,与它的增广矩阵是一一对应的. 例如,线性方程组 
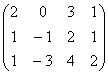
|
|
2、 解线性方程组的公式法 如果线性方程组满足两个条件: (1)方程组中未知量的个数等于方程的个数, (2)系数行列式不为零, 则可以用克莱姆法则中给出的公式解线性方程组. |
|
3、解线性方程组的消元法 用消元法解线性方程组. 以二元线性方程组  为例,设其为方程组(1). 为例,设其为方程组(1).对换其中两个方程,得方程组(2): 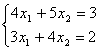
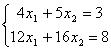
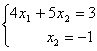
解题过程中的方程组(1)、(2)、(3)、(4)都是同解方程组. 可见:线性方程组经过下列三种变换得到的新方程组与原方程组是同解的: (1)交换两个方程; (2)将某个方程乘以一个不为零的常数; (3)将某个方程乘以一个数加到另一个方程上去. |
|
设想: 解方程组时,在所有与该方程组同解的方程组中,找出最简单的一个,通过它求出原方程组的解. 方法: 对线性方程组的增广矩阵作相应的运算,即初等行变换,每变换一次,得到的新矩阵都对应原方程组的一个同解方程组.当增广矩阵变为行最简矩阵时,该行最简矩阵对应的方程组就是我们需要的最简方程组. |
|
典型例题 例6.4.1 解三元线性方程组  . .解 方法1 因为方程组中,方程的个数=未知量的个数=3,且系数行列式 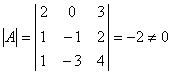 ,所以,可用克莱姆法则的公式求解.(解法略) ,所以,可用克莱姆法则的公式求解.(解法略)方法2 利用初等行变换. 增广矩阵为 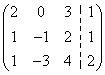
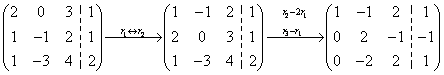

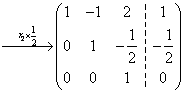 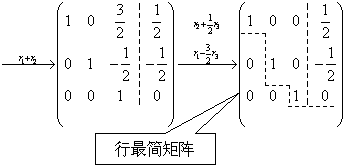
由此得方程组的解 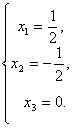 . . |
|
例6.4.2 求解线性方程组 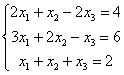 . .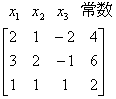 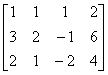
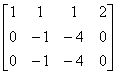
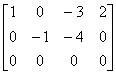

所以原方程组化简为 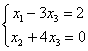 , ,故原方程组的通解为 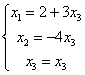 , ,思考:此题是否可用公式法?请同学们自行分析一下. |
|
可以算出系数行列式  , , |
|
例6.4.3 求解线性方程组 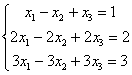 . .
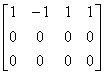
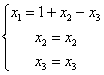 , , |
|
例6.4.4 求解线性方程组 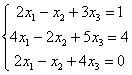 . .

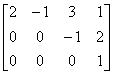
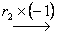

所以原方程组化简为  , , |
|
例6.4.5 试问当 
解 方程组的系数矩阵  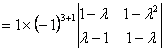
故由克莱姆法则知,当 当 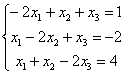 , ,
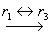
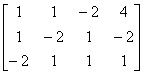
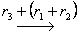

以上矩阵的最后一行相当于方程组中出现了方程 当  , ,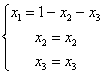 . . |
|
请认真答题,测试一下你对前面知识点的学习情况!
24.(单选题)线性方程组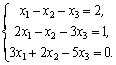 的解为( )
的解为( )
【答案】D
【解析】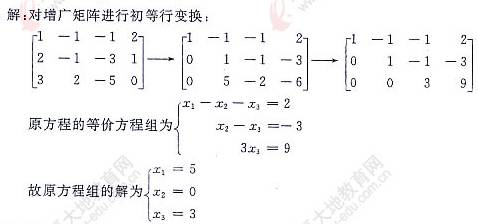
【知识点】解线性方程组的消元法