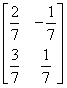
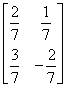
6.6 逆矩阵
一、方阵可逆及逆阵的定义
(1)可逆阵一定是方阵,但不是所有方阵均可逆. (2)当 (3)若 证 设 |
二、方阵可逆的充分必要条件充要条件 1 若AB=E(或BA=E),则 充要条件 2 方阵
两个充要条件的应用 (1)判断一个方阵是否可逆. (2)证明某矩阵是另一个矩阵的逆阵. |
|
典型例题 例6.6.1 证明下列命题成立 (1)若 (2)若 证明: (1)∵ ∴ (2)∵ ∴ |
|
例6.6.2 设 证明 由已知条件可知, 进一步有 |
|
例6.6.3 设 证 因为 在等式 |
三、如何求可逆方阵的逆阵1、 伴随矩阵
(1) 矩阵 (2) 伴随矩阵具有性质 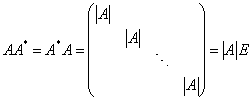
|
|
2 、 利用伴随矩阵求方阵的逆阵
|
|
典型例题 例6.6.4 讨论矩阵 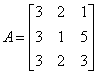 的可逆性.如果可逆,求出其逆矩阵. 的可逆性.如果可逆,求出其逆矩阵.解 因为  , ,由于 所以 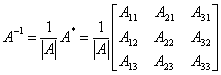
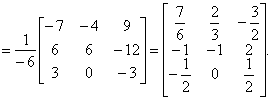
|
|
例6.6.5 设二阶方阵 解 因为 由于 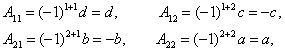
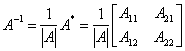
例如,设 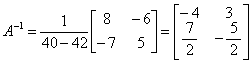 . . |
四、可逆方阵的性质
|
五、逆阵的应用1 、利用逆阵求解矩阵方程 (1) 设矩阵方程为 (2) 设矩阵方程为 (3) 设矩阵方程为 |
|
2 、利用逆阵求解线性方程组(当方程个数和未知量个数相等时) 线性方程组可用矩阵方程 于是,当系数矩阵 注:利用逆阵求解线性方程组是有条件的,首先系数矩阵必须是方阵,即方程组所含方程的个数与未知量的个数必须相等;其次系数矩阵还必须是可逆的.这和运用克莱姆法则解线性方程组的条件是一致的. |
|
典型例题 例6.6.6 解线性方程组 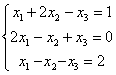
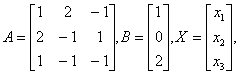 则方程组改写成矩阵方程 则方程组改写成矩阵方程因为 
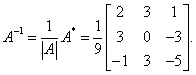
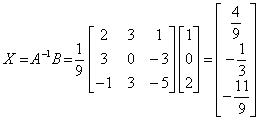 . .
|
|
请认真答题,测试一下你对前面知识点的学习情况!
25.(单选题)设A=![]() ,则A-1=( )
,则A-1=( )
【答案】C
【解析】A-1=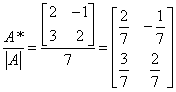
【知识点】利用伴随矩阵求方阵的逆阵
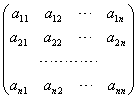 ,其行列式
,其行列式