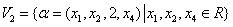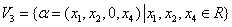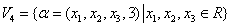第三章 向量空间
一、n 维向量线性运算的定义和性质
例1 已知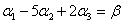 其中,
其中,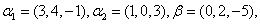
则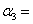 ____________.
____________.
测试点 n 维向量线性运算的定义和性质
解 因为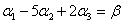 ,所以
,所以
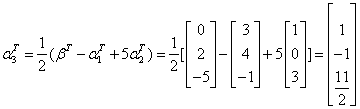
故 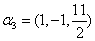 (请验算)
(请验算)
答案 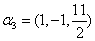 .
.
例2 设向量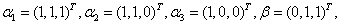 则
则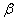 由
由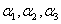 线性表出的表示式为_____________.
线性表出的表示式为_____________.
测试点 向量由向量组线性表示;组合系数的求法
解 考虑 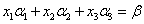
该线性方程组的增广矩阵


所以 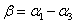
答案 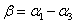 (验算!)
(验算!)
二、n 维向量组的线性相关性
1.向量组的线性相关性的定义和充分必要条件:
1)定义: 设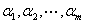 是一组n维向量.如果存在m个不全为零的数
是一组n维向量.如果存在m个不全为零的数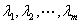 ,使得
,使得
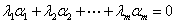 ,
,
则称向量组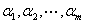 线性相关,否则,即如果
线性相关,否则,即如果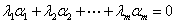 ,必有
,必有
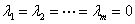 ,则称向量组
,则称向量组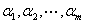 线性无关.
线性无关.
2) m 个n 维向量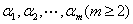 线性相关的充分必要条件是至少存在某个
线性相关的充分必要条件是至少存在某个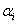 是其余向量的线性组合.即
是其余向量的线性组合.即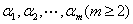 线性无关的充分必要条件是其中任意一个向量都不能表示为其余向量的线性组合.
线性无关的充分必要条件是其中任意一个向量都不能表示为其余向量的线性组合.
例3 设向量组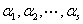 线性相关,则必可推出( )
线性相关,则必可推出( )
A.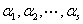 中至少有一个向量为零向量
中至少有一个向量为零向量
B.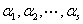 中至少有两个向量成比例
中至少有两个向量成比例
C.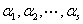 中至少有一个向量可以表示为其余向量的线性组合
中至少有一个向量可以表示为其余向量的线性组合
D.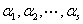 中每一个向量都可以表示为其余向量的线性组合
中每一个向量都可以表示为其余向量的线性组合
测试点 向量组线性相关的概念
答案 C
例4 向量组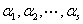 线性无关的充分条件是
线性无关的充分条件是
A. 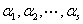 都不是零向量
都不是零向量
B. 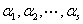 中任意两个向量都不成比例
中任意两个向量都不成比例
C. 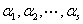 中任意一个向量都不能表为其余向量的线性组合
中任意一个向量都不能表为其余向量的线性组合
D. 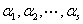 中任意
中任意 个向量都线性无关
个向量都线性无关
测试点 向量组线性相关的概念; 充分条件;必要条件;充分必要条件.
解 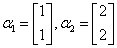 都不是零向量,但
都不是零向量,但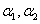 线性相关.
线性相关.
 中任意两个向量都不成比例,且其中任意3-1=2个向量都线性无关,但
中任意两个向量都不成比例,且其中任意3-1=2个向量都线性无关,但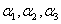 线性相关.故A,B,D都不正确.
线性相关.故A,B,D都不正确.
答案 C
例5.设向量组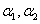 线性无关,证明向量组
线性无关,证明向量组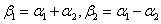 也线性无关.
也线性无关.
测试点 向量组线性无关的定义;
证 设 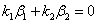
因为 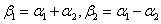
则 
即 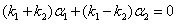
因为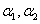 线性无关,故
线性无关,故 ,所以只能
,所以只能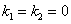 .
.
这表明若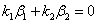 ,必有
,必有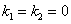 .据向量组线性无关的定义,知
.据向量组线性无关的定义,知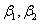 也线性无关
也线性无关
例6.若向量组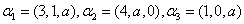 线性无关,则
线性无关,则 可能的取值应满足 .
可能的取值应满足 .
测试点 n 个 n 维向量线性无关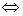 相应的行列式
相应的行列式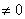 ;
;
解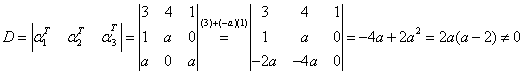
所以 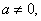 且
且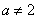 .
.
答案 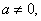 且
且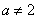 .
.
请认真答题,答题结果将记入知识点测评的成绩!
【单选题】12.若向量组 线性相关,则实数
线性相关,则实数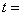 ( )。
( )。
【答案】B
【解析】 =0
=0
解得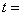 1
1
【知识点】n 个n 维向量线性无(相)关的充分必要条件
2. 关于线性相关的几个定理
1) 如果向量组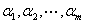 线性无关,而
线性无关,而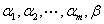 线性相关,则
线性相关,则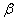 可由
可由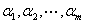 线性表示,且表示法唯一.
线性表示,且表示法唯一.
2) 线性相关的向量组再增加向量所得的新向量组必线性相关.(部分相关,则整体相关;或整体无关,则部分无关)
3) 若向量组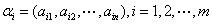 线性无关,则接长向量组
线性无关,则接长向量组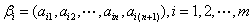
必线性无关.
3.判断向量组线性相关性的方法
1)一个向量 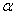 线性相关
线性相关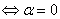 ;
;
2)含有零向量的向量组必线性相关;
3)向量个数=向量维数时,n维向量组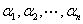 线性相关
线性相关
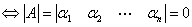 .
.
4)向量个数>向量维数时, 向量组必线性相关;
5)部分相关,则整体必相关;(整体无关,则部分必无关).
6)若向量组线性无关,则其接长向量组必线性无关;
7)向量组线性无关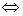 向量组的秩=所含向量的个数,向量组线性相关
向量组的秩=所含向量的个数,向量组线性相关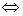 向量组的秩<所含向量的个数;
向量组的秩<所含向量的个数;
8)向量组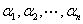 线性相关(无关)的充分必要条件是齐次方程组
线性相关(无关)的充分必要条件是齐次方程组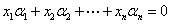
有(没有)非零解.
例7 设 n 维向量组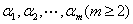 线性无关,则
线性无关,则
A.组中减少任意一个向量后仍线性无关
B.组中增加任意一个向量后仍线性无关
C.存在不全为零的数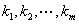 ,使
,使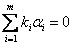
D.组中至少有一个向量可以由其余向量线性表出
解析 因为若向量组线性相关,则增加任何一个向量后仍线性相关,其等价的定理是向量组相性无关,则组中减少任意一个向量后仍线性无关
答案 A
例8 设向量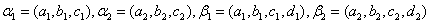 ,下列命题中正确的是( )
,下列命题中正确的是( )
A.若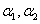 线性相关,则必有
线性相关,则必有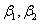 线性相关
线性相关
B.若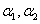 线性无关,则必有
线性无关,则必有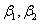 线性无关
线性无关
C.若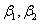 线性相关,则必有
线性相关,则必有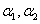 线性无关
线性无关
D.若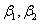 线性无关,则必有
线性无关,则必有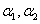 线性相关
线性相关
答案 B
例9 设向量组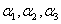 线性无关,而向量组
线性无关,而向量组 线性相关.证明:向量
线性相关.证明:向量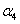 必可表为
必可表为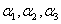 的线性组合.
的线性组合.
测试点 关于线性相关性的几个定理
证1因为 线性相关,故
线性相关,故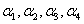 线性相关,又因为
线性相关,又因为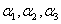 线性无关,所以
线性无关,所以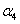 必可表为
必可表为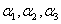 的线性组合.
的线性组合.
证毕.
证2 因为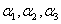 线性无关,故
线性无关,故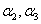 必线性无关,又因为
必线性无关,又因为 线性相关
线性相关
故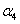 必能由
必能由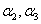 线性表示,当然可表为
线性表示,当然可表为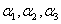 的线性组合.
的线性组合.
证毕.
请认真答题,答题结果将记入知识点测评的成绩!
【单选题】13. 设向量组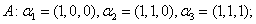
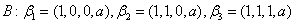 下列命题中正确的是( )。
下列命题中正确的是( )。
【答案】C
【解析】因为 ,故向量组A线性无关.而向量组B是向量组A的接长向量组,所以向量组B也线性无关。
,故向量组A线性无关.而向量组B是向量组A的接长向量组,所以向量组B也线性无关。
【知识点】关于线性相关性的几个定理
三、向量组的极大无关组及向量组的秩
1.极大无关组的定义:
设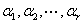 是向量组
是向量组 的一个部分组.如果(1)
的一个部分组.如果(1)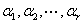 线性无关;(2)任给
线性无关;(2)任给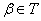 ,都有
,都有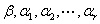 线性相关,则称
线性相关,则称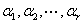 是向量组T的一个极大无关组.
是向量组T的一个极大无关组.
2.向量组的秩,向量组的秩与矩阵的秩;求向量组的极大无关组,并将其余向量由该极大无关组线性表示的的方法
例10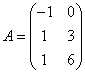 的行向量组的秩=____________.
的行向量组的秩=____________.
测试点 矩阵的秩与向量组的秩之间的关系;
答案 2
例11 设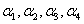 是一个4维向量组,若已知
是一个4维向量组,若已知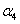 可以表为
可以表为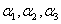 的线性组合,且表示法惟一,则向量组
的线性组合,且表示法惟一,则向量组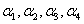 的秩为( )
的秩为( )
A.1 B.2
C.3 D.4
测试点 (1)向量组的秩的概念;(2)向量由向量组线性表示的概念 (3)向量组线性相关和线性无关的概念
解 因为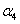 可以表为
可以表为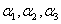 的线性组合,且表示法惟一,必有
的线性组合,且表示法惟一,必有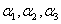 线性无关,因为
线性无关,因为
设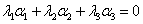 ,由
,由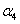 可以表为
可以表为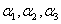 的线性组合,即
的线性组合,即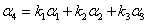
故 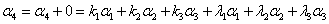
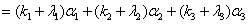
由表示法惟一,有
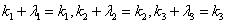
于是有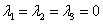 ,故
,故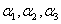 线性无关,又
线性无关,又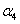 可以表为
可以表为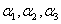 的线性组合,所以
的线性组合,所以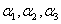 为向量组
为向量组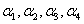 的一个极大无关组,故向量组
的一个极大无关组,故向量组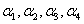 的秩为3.
的秩为3.
答案 C
例12 设向量组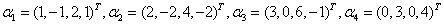
(1)求向量组的秩和一个极大线性无关组;
(2)将其余向量表为该极大线性无关组的线性组合.
测试点 求向量组的极大无关组,并将其余向量由该极大无关组线性表示的的方法
解 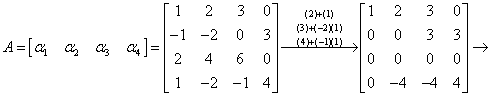
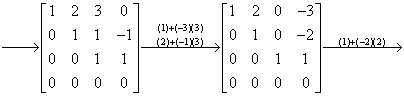
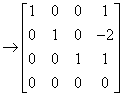
所以,原向量组的秩为3, 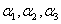 为所求的极大无关组.
为所求的极大无关组.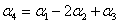
请认真答题,答题结果将记入知识点测评的成绩!
【单选题】14. 向量组  则该向量组的秩为( )。
则该向量组的秩为( )。
【答案】B
【解析】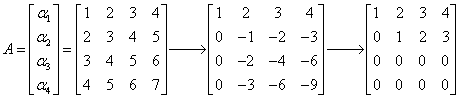
所以该向量组的秩为2。
【知识点】向量组的秩
四、子空间的定义,基、维数、向量在一组基下的坐标
1. n 维向量空间的定义:n 维实向量的全体构成的集合称为n 维向量空间,记为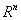 .
.
2. 子空间的定义:设V是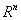 的一个非空子集,且满足对加法运算和数乘运算封闭,则称V是
的一个非空子集,且满足对加法运算和数乘运算封闭,则称V是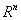 的一个子空间,简称为向量空间V.
的一个子空间,简称为向量空间V.
3.生成子空间的定义:设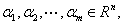 则由它们的所有线性组合构成
则由它们的所有线性组合构成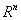 的一个子空间,称它为由
的一个子空间,称它为由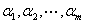 生成的子空间.
生成的子空间.
例13 设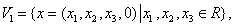

 ,说明哪个是子空间,那个不是.
,说明哪个是子空间,那个不是.
解析 在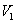 中,任取
中,任取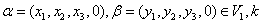 为任意数,都有
为任意数,都有
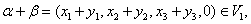
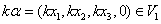
所以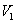 是子空间.
是子空间.
类似地,可以证明 也是子空间.
也是子空间.
但对 ,取
,取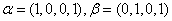 都属于
都属于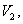 而
而
 这表明
这表明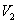 对加法运算不封闭,故
对加法运算不封闭,故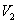 不是子空间.
不是子空间.
请认真答题,答题结果将记入知识点测评的成绩!
【单选题】15. 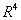 的下列子集中( )是子空间。
的下列子集中( )是子空间。
【答案】C
【解析】在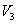 中,任取
中,任取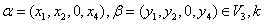 为任意数,都有
为任意数,都有
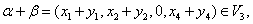
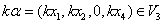
所以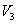 是子空间.
是子空间.
但对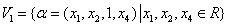 ,取
,取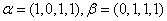 都属于
都属于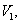 而
而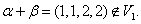 这表明
这表明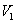 对加法运算不封闭,故
对加法运算不封闭,故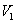 不是子空间.
不是子空间.
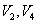 也不是子空间。
也不是子空间。
【知识点】子空间的定义
4. 向量空间的基和维数的定义
向量空间V的一个向量组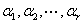 线性无关,且V中每个向量都能由它线性表示,则称它为向量空间的一个基.零空间
线性无关,且V中每个向量都能由它线性表示,则称它为向量空间的一个基.零空间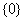 没有基,定义它为0维,否则,称向量空间的基所含向量个数 r 为该空间的维数.设
没有基,定义它为0维,否则,称向量空间的基所含向量个数 r 为该空间的维数.设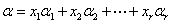
称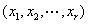 为
为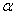 在这组基下的坐标.
在这组基下的坐标.
例14向量空间 为实数}的维数为_______________.
为实数}的维数为_______________.
测试点 向量空间维数的概念
解 容易看出 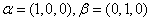 是V的一个基。
是V的一个基。
答案 2
例15证明向量组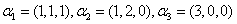 是
是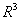 的一组基,则向量
的一组基,则向量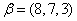 在这组基下的坐标是____________.
在这组基下的坐标是____________.
测试点 向量在一组基下的坐标
解 因为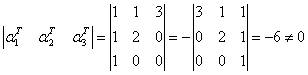
故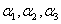 线性无关,所以它是
线性无关,所以它是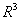 的一组基.
的一组基.
考虑 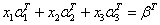
该线性方程组的增广矩阵为

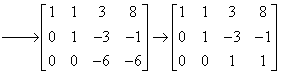
得 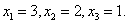
所以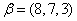 在这组基下的坐标是
在这组基下的坐标是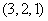 (即
(即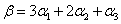 )
)
答案 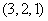 .
.
例16 求由向量组 生成的子空间的一个基,并说明该生成子空间的维数.
生成的子空间的一个基,并说明该生成子空间的维数.
解析 显然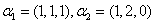 是
是 的一个极大无关组,故是由向量组
的一个极大无关组,故是由向量组 生成的子空间的一个基,所以该子空间的维数等于2。
生成的子空间的一个基,所以该子空间的维数等于2。
请认真答题,答题结果将记入知识点测评的成绩!
【单选题】16. 子空间 的维数为( )。
的维数为( )。
【答案】C
【解析】因为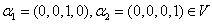 ,线性无关,且任给
,线性无关,且任给
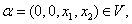 必有
必有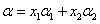 。所以
。所以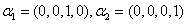 是
是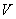 的一组基,故
的一组基,故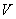 的维数等于
的维数等于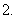
【知识点】向量空间的维数
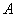 线性相关,向量组
线性相关,向量组 线性相关
线性相关