例3 设3阶矩阵A的每行元素之和均为2,则A必有一个特征值为 .
测试点1. 特征值的定义 2.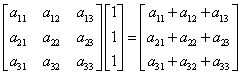
解 因为3阶矩阵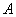 的每行元素之和均为2,
的每行元素之和均为2,
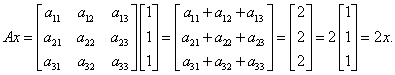
所以A必有一个特征值为2.
答案 2
例4 设矩阵 ,则A的线性无关的特征向量的个数是( )
,则A的线性无关的特征向量的个数是( )
A. B.
B.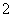
C.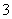 D.
D.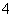
解 A的特征值为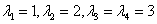 ,当
,当 时,
时,

所以 ,故(3E-A)x=0的基础解系只含一个解,这表明A只有一个属于特征值3的线性无关的特征向量,故A的线性无关的特征向量的个数是3.
,故(3E-A)x=0的基础解系只含一个解,这表明A只有一个属于特征值3的线性无关的特征向量,故A的线性无关的特征向量的个数是3.
答案 C
二、相似矩阵
1.相似矩阵的定义
设A,B都是n阶方阵,如果存在可逆阵P,使得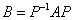 ,则称A与B相似.
,则称A与B相似.
2. 相似矩阵的性质
1)反身性,对称性,传递性;
2)若方阵A与B相似,则A与B有相同的特征值,(但不一定有相同的特征向量)进而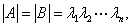 ,且
,且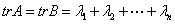 ,其中
,其中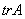 表示矩阵A的迹,即
表示矩阵A的迹,即 ,
,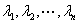 为方阵A的n个特征值;
为方阵A的n个特征值;
注意:反之,若A与B有相同的特征值,A与B不一定相似;例如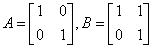 有相同的特征值,但A与B不相似.
有相同的特征值,但A与B不相似.
例8 设3阶矩阵A与B相似,且已知A的特征值为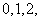 则矩阵B的迹
则矩阵B的迹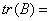 ( )
( )
A. 3 B. 2 C.1 D.0
测试点
1. 相似矩阵的特征值相同;从而其迹和行列式也相同;
2.矩阵的特征值与该矩阵的迹和行列式的关系.
解 由已知B的特征值也为0,1,2,故B的迹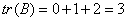
答案 A
例9 设3阶矩阵A与B相似,且已知A的特征值为2,2,3, 则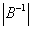 =( )
=( )
A.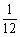 B.
B.
C.7 D.12
测试点
(1) 相似矩阵的特征值相同;
(2)设 为矩阵A的一个特征值,则
为矩阵A的一个特征值,则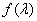 为矩阵
为矩阵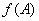 的特征值;
的特征值; 为矩阵
为矩阵 的特征值.
的特征值.
(3)矩阵的特征值与该矩阵的迹和行列式的关系.
解 因为3阶矩阵A与B相似,所以B与A有相同的特征值,所以B的特征值为2,2,3,故
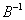 的特征值为
的特征值为 从而
从而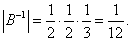
答案 A
例10 若2阶矩阵A相似于矩阵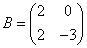 ,E为2阶单位矩阵,则与矩阵E-A相似的矩阵是( )
,E为2阶单位矩阵,则与矩阵E-A相似的矩阵是( )
A.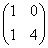 B.
B.
C. D.
D.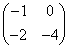
测试点 相似矩阵的概念;相似矩阵的性质(若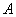 与
与 相似,则
相似,则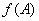 与
与 相似;相似矩阵有相同的特征值等);三角形矩阵的特征值
相似;相似矩阵有相同的特征值等);三角形矩阵的特征值
解1 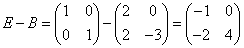 ,故E-B的特征值为
,故E-B的特征值为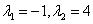 .因为A与B相似,故E-A与E-B相似,所以,凡与矩阵E-A相似的矩阵的特征值都是-1,4,故在A,B,C,D四个选项中,正确的只能是C.
.因为A与B相似,故E-A与E-B相似,所以,凡与矩阵E-A相似的矩阵的特征值都是-1,4,故在A,B,C,D四个选项中,正确的只能是C.
解2 因为二阶方阵E-A有两个不同的特征值,故E-A与对角阵 相似,同理
相似,同理 也与对角阵
也与对角阵 相似,故E-A与
相似,故E-A与 相似.
相似.
答案 C
3.方阵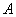 的对角化问题
的对角化问题
1)n阶方阵A能与对角阵相似的充分必要条件是A有n个线性无关的特征向量;设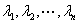 是方阵A的n个特征值,
是方阵A的n个特征值,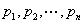 依次是方阵A的属于特征值
依次是方阵A的属于特征值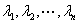 的n个线性无关的特征向量.若令
的n个线性无关的特征向量.若令 ,则
,则
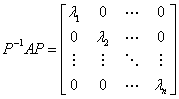 .
.
2)若方阵A有n个不同的特征值(即特征方程无重根),则A必能与对角阵相似.(这是A能与对角阵相似的充分条件,不是必要条件)
例11 n阶矩阵A与对角阵相似的充分必要条件是( )
A 矩阵A有n个特征值 B 矩阵A有n个线性无关的特征向量
C 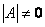 D 矩阵A的特征多项式没有重根
D 矩阵A的特征多项式没有重根
答案 B
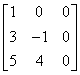
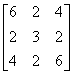
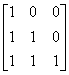
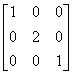
例12 判断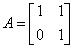 能否与对角阵相似.
能否与对角阵相似.
解析 
故(E-A)x=0的基础解系只含一个解,即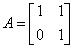 只有一个线性无关的特征向量,故
只有一个线性无关的特征向量,故
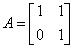 不能与对角阵相似.
不能与对角阵相似.
三.向量的内积和正交矩阵
1.向量内积的定义:设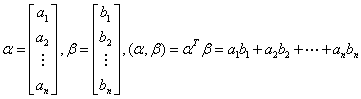
2.向量的长度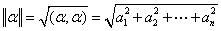
3.单位化向量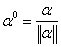
4.正交向量组的定义及其性质
定义 如果一个向量组不含零向量,且其中任意两个向量都正交(简称两两正交),则称该向量组为正交向量组.
主要性质 正交向量组必线性无关
5.施密特正交化手续
例18 已知3维向量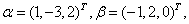 则内积
则内积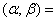 ____________.
____________.
测试点 内积的定义
解 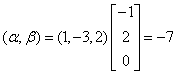
答案 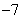
例19 求一个单位向量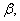 使得
使得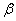 与
与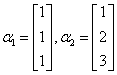 都正交.
都正交.
解 设 与
与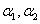 都正交,则
都正交,则
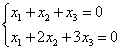
可取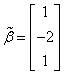 ,单位化得
,单位化得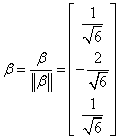 即为所求.
即为所求.
例20 利用施密特正交化方法,将下列向量组化为正交的单位向量组:
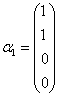 ,
, 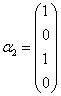 .
.
测试点 施密特正交化手续
解 取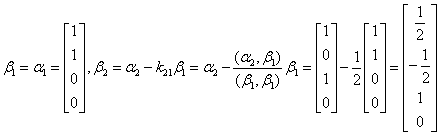
则 为所求的单位正交向量组.
为所求的单位正交向量组.
验算
四.实对称矩阵的相似标准形
1.实对称矩阵的特征值都是实数;
2.实对称矩阵属于不同特征值的特征向量相互正交;
3.实对称矩阵必能与对角阵相似,且存在正交阵P,使得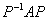 为对角形.
为对角形.
4.任给实对称阵A,如何求出正交阵P,使得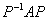 为对角形.
为对角形.
例21设3阶实对称矩阵A的特征值为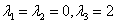 ,则秩(A)=( )
,则秩(A)=( )
A. B.
B.
C.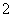 D.
D.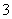
测试点
1.相似矩阵与等价矩阵的概念;
2.等价矩阵有相等的秩;
3.阶梯形矩阵的秩
解 因为3阶实对称矩阵A的特征值为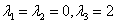 ,故矩阵A必与对角阵
,故矩阵A必与对角阵 相似,所以A必与对角阵
相似,所以A必与对角阵 等价,所以秩(A)=1.
等价,所以秩(A)=1.
答案 B
 是n阶方阵A的特征值,是指存在非零列向量
是n阶方阵A的特征值,是指存在非零列向量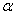 ,使得
,使得 .这时,称
.这时,称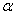 为矩阵A属于特征值
为矩阵A属于特征值 的特征向量.由此知,
的特征向量.由此知, 是n阶方阵A的特征值
是n阶方阵A的特征值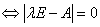 ,这时,齐次方程组
,这时,齐次方程组 的非零解都是矩阵A属于特征值
的非零解都是矩阵A属于特征值 的特征向量.
的特征向量. B.
B. C.
C. 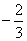 D.
D. 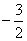
 为A的特征值的充分必要条件是
为A的特征值的充分必要条件是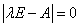 .
.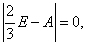 所以A必有一个特征值为
所以A必有一个特征值为 .
.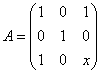 的一个特征值为
的一个特征值为 ,则
,则 ____________.
____________. 为A的特征值的充分必要条件是
为A的特征值的充分必要条件是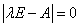 .
. 为矩阵
为矩阵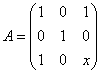 的一个特征值
的一个特征值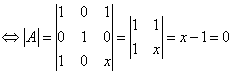
 .
.
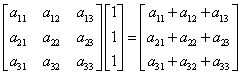
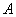 的每行元素之和均为2,
的每行元素之和均为2, 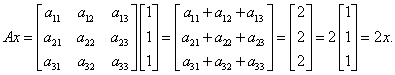
 ,则A的线性无关的特征向量的个数是( )
,则A的线性无关的特征向量的个数是( )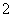
 D.
D.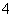
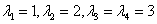 ,当
,当 时,
时, 
 ,故(3E-A)x=0的基础解系只含一个解,这表明A只有一个属于特征值3的线性无关的特征向量,故A的线性无关的特征向量的个数是3.
,故(3E-A)x=0的基础解系只含一个解,这表明A只有一个属于特征值3的线性无关的特征向量,故A的线性无关的特征向量的个数是3. 的非零特征值为( )。
的非零特征值为( )。
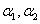
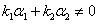
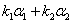
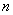
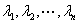
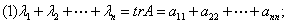

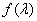
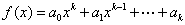
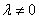



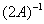 必有一个特征值为_____________.
必有一个特征值为_____________. .
.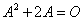
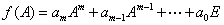
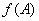
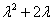
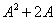

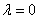
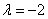
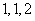 ,则
,则 ( )。
( )。 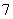

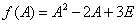 ,则
,则

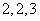
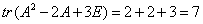 。
。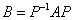
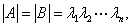
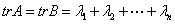
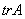

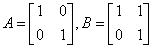
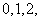
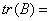
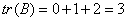
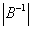
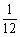

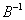

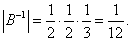
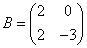
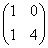


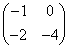


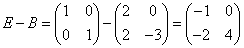
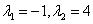

 的特征向量.则下列命题错误的是( )。
的特征向量.则下列命题错误的是( )。

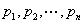 依次是方阵
依次是方阵 ,则
,则  .
.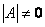 D 矩阵
D 矩阵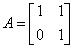 能否与对角阵相似.
能否与对角阵相似.
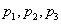
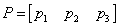
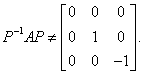
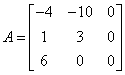
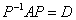
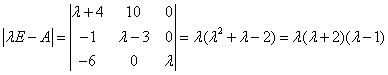
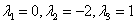


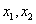



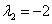
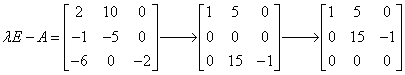
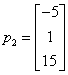
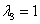

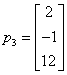
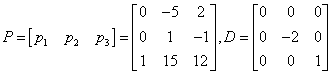
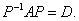
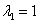

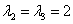

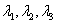


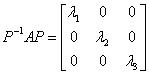




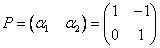
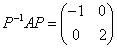





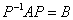

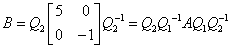
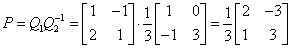
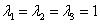 ,而
,而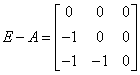 的秩为
的秩为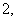 故矩阵
故矩阵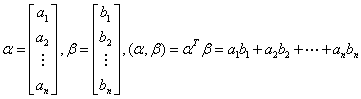
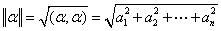
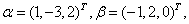
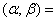
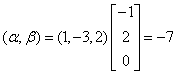
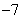
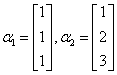

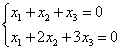
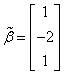
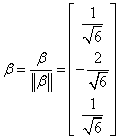
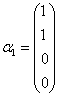
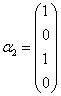
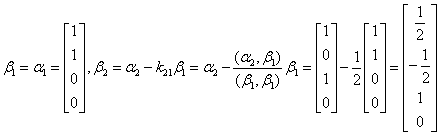

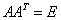
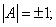
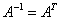
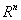
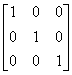
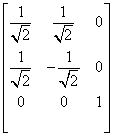
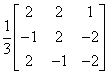
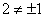 ,故它不是正交阵。
,故它不是正交阵。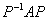
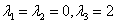

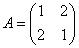
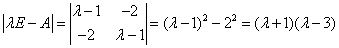
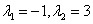
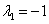
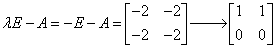
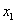
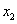
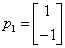
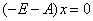
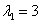
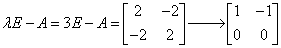
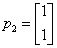

 =( )。
=( )。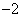
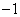
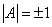 ,所以
,所以 .
.