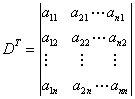1.3 行列式的性质与计算
一、行列式的性质
|
首先介绍转置行列式的概念。
例如 性质1表明:在行列式中,行与列的地位是平等的或对称的,因而行列式有关于行的性质,对列也同样成立。 性质 2 :用数 k 乘行列式 D 中某一行(或某一列)所得的行列式等于行列式 D 的 k 倍,换句话说,对行列式,可以按行(列)提出公因数。 例如 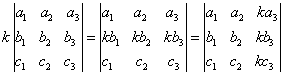
|
| 例 1:计算行列式 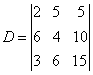
解:D中第二行元素有公因数2,第三行元素有公因数3,都可提出来,即 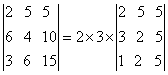
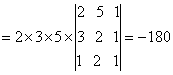
|
|
性质 3: 互换行列式的任意两行(或两列),行列式的值变号 例如 
推论 1 :若行列式中有某两行(列)相同,则此行列式为零。 推论 2 :若行列式中有某两行(列)元素对应成比例,则此行列式为零。 例如 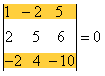
这是因为第一行元素与第三行元素对应成比例。 性质 4 :若行列式的某一行(或某一列)的每一元素均表为两个数的和,则行列式可以按该行(列)拆成两个行列式相加。 例如 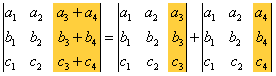
注意:在拆成两个行列式相加时,应逐行或逐列拆,即  , ,应该为 

性质 5 :把行列式 D 的某一行(列)的 k 倍加到另一行(列)上,行列式的值不变。 例如 

|
|
例 2:已知104,273,351均能被13整除, 证明:行列式 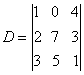 也能被13整除 也能被13整除证:把D的第一列的100倍,第二列的10倍均加到第三列上,得 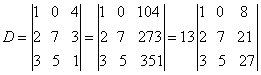 ,而 ,而 的值必是整数。 的值必是整数。所以D的值为13的整数倍,即D能被13整除。证毕。 |
|
例 3:证明 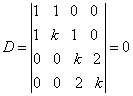 的充要条件是 的充要条件是证: 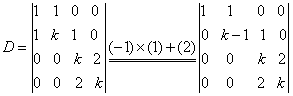
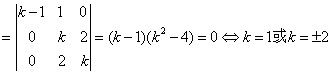
证毕。 |
|
由以上行列式性质与展开定理,可得
|
二、行列式的计算
|
行列式的计算主要有以下两种基本方法 ( 1 )利用行列式性质,把原行列式化为上(下)三角行列式求值。 ( 2 )利用性质,先把行列式中某一行(或某一列)的元素尽可能多的化为零,然后再按该行或列展开,把阶数逐步降下来。 |
|
例 4:计算行列式 
解:方法一,化为上三角行列式 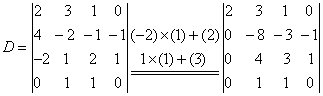


由于D中第4列已有两个元素为零,利用性质5,再把一个元素化为零。 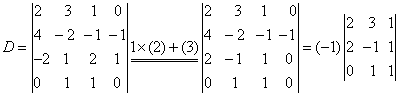
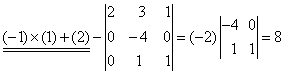
|
|
例5:计算n阶行列式 
解 方法一 这个行列式的特点是每行元素的和均为 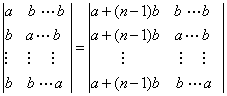
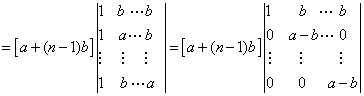
方法二考虑到D中每一行上有很多元素为b,采用“加边法”,即造一个与D相等的n+1阶行列式。 当 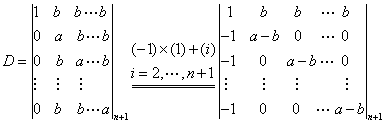

|
|
例6:计算行列式 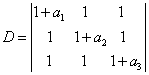
解:方法一,直接按第一列展开 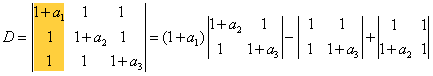
方法二 降阶法 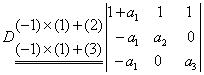

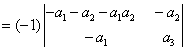
方法三 加边法 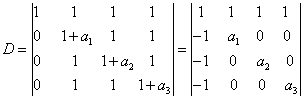
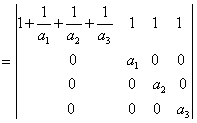
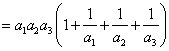
|
请认真答题,测试一下你对前面知识点的学习情况!
(单选题) 1.设行列式 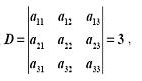
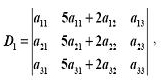 则 D1的值为( )
则 D1的值为( )
【答案】C
【解析】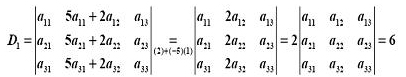
【知识点】行列式的性质
请认真答题,测试一下你对前面知识点的学习情况!
(单选题) 2.计算行列式 =( )
=( )
【答案】C
【解析】:

【知识点】行列式的计算
 ,则
,则