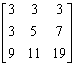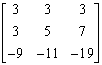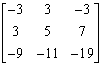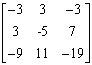2.2 矩阵的运算
一、矩阵的加法
例如 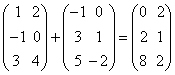
由定义知:只有同型矩阵才可以相加,且矩阵加法实质上是对应元素相加,与两个行列式相加有本质区别。 矩阵加法满足下列运算律: (1)交换律 (2)结合律 (3) (4)消去律 (5)设 例如: |
二、数量乘法
例如 由定义可知:数k与矩阵A的数乘运算是用k去乘A中每一个元素,它与数k与行列式的相乘又是完全不相同的。 矩阵的数乘运算满足下列运算律: (1)结合律 (2)分配律 |
|
例1:已知 解: 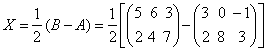
|
三、矩阵的乘法
|
先看一个例子: 设 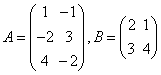 ,我们来求AB(说A为左矩阵,B为右矩阵)。矩阵乘法的关键是:左矩阵的 ,我们来求AB(说A为左矩阵,B为右矩阵)。矩阵乘法的关键是:左矩阵的
行与右矩阵的列对应相乘再相加,现把A的三个行与B的两个列分别对应相乘再相加后得到矩阵: 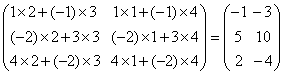
这就是A乘以B的乘积矩阵,即: 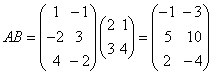
由此例可知:欲进行矩阵A与B的乘法运算,必须要求左矩阵A的列数与右矩阵B的行数相同,而乘积矩阵的行数就是左矩阵的行数,乘积矩阵的列数就是右矩阵的列数。
|
|
例2:设 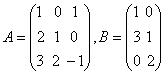 。求AB与BA。 。求AB与BA。解:先求AB,这里A作为左矩阵是3×3矩阵,B作为右矩阵是3×2矩阵,因而AB是有意义的。 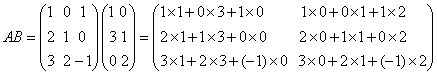 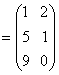
而BA没有意义,因为B的列数与A的行数不相同。 例3:设 解:由A与B均为2阶方阵,所以AB与BA都有意义。 |
|
由矩阵乘法定义以及上述例题,矩阵的乘法与两个普通数的乘法是有所不同的。 注意: (ⅰ)一般情况下,矩阵乘法不满足交换律,即一般地 (ⅱ)由AB=0并不能推出A=0或B=0,因而不满足消去律,即由AB=AC,一般地不能推出B=C。 我们只是说一般地, 显然只有同阶方阵才可能是可交换的。 矩阵乘法满足下列运算律。 (1)结合律 (2)分配律 (3)与数乘的结合律 (4) |
|
例4:设 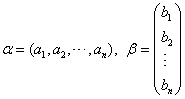 ,求 ,求解: 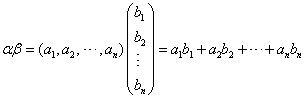
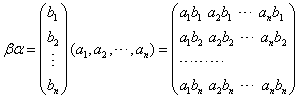
|
|
由矩阵乘法,我们给出线性方程组的矩阵表示: 设有线性方程组: 
引进系数矩阵 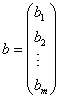 ,未知量列向量 ,未知量列向量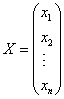
则线性方程组(1.2)可写成如下矩阵形式: |
四、方阵的方幂与多项式
例5:设A、B均为n阶矩阵,证明:(1) (2) 证:(1) 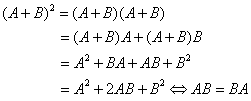
(2)的证明类似。 例6:(1)由 (2)由 解:均是错误的,例如: (1) (2) 有 |
注意:方阵多项式中,末项为数量矩阵 例7:设 解: 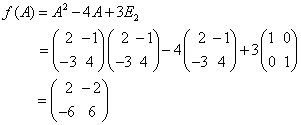
|
五、矩阵的转置
例如 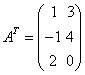
例8:已知A为 证:设B为 则 所以B为 |
|
矩阵的转置运算满足下列运算律: (1) (2) (3) (4) 例9:设 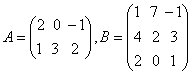 ,验证 ,验证证: 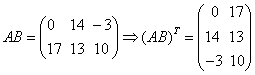

所以 |
例如  均为对称矩阵, 均为对称矩阵,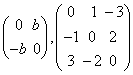 均为反对称矩阵。 均为反对称矩阵。例10:设A为n阶对称矩阵,P为任一个n阶方阵,证明: 解:由A为对称矩阵,有 反之,由 |
六、方阵的行列式
|
由行列式与矩阵的定义,矩阵与行列式是两个完全不同的概念,不同之处在于: (1)矩阵是一个数表,行列式是一个数,而且行列式记号“ (2)矩阵的行数与列数未必相等,但行列式的行数与列数必须相等。 但是,对于n阶方阵,我们可以把它与行列式联系。
例如 又显然单位方阵E的行列式 |
|
方阵的行列式具有以下性质: 设A,B为n阶方阵,k为任一个数,则 (1) (2) (3) 但要注意,一般地 例11:设 证: 所以 |
请认真答题,测试一下你对前面知识点的学习情况!
(单选题) 5.设矩阵![]() ,
, ![]() ,则
,则![]() =( )。
=( )。
【答案】C
【解析】
【知识点】矩阵的转置
请认真答题,测试一下你对前面知识点的学习情况!
(单选题)6.设A为3阶方阵,且|A|=2,则|2A-1|=( )
【答案】D
【解析】 ![]()
【知识点】方阵的行列式