2.3 方阵的逆矩阵
一、可逆矩阵与逆矩阵
| 我们已知,对于任意一个非零数
|
|
说明:(1)由定义,说A是可逆矩阵,要求A与其逆矩阵 (2)“可逆矩阵”的含义就是“可以存在逆矩阵的矩阵”。 (3)当A为可逆矩阵,其逆矩阵是唯一的,故可以记为 例如设 |
二、矩阵可逆的条件与逆矩阵的求法
注意:伴随矩阵 在A与 例1:设二阶方阵 解: 故 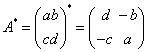
求二阶方阵的伴随矩阵的口诀:“主交换,次变号” |
证明(必要性) 设A为可逆矩阵,则存在B,使AB=E,两边取行列式,得 设 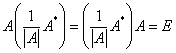 ,由矩阵可逆的定义,A可逆,且 ,由矩阵可逆的定义,A可逆,且本定理给出了用伴随矩阵求逆矩阵的方法。 |
|
例2:判断 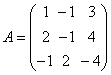 是否可逆?若可逆,求 是否可逆?若可逆,求解:由 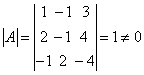 ,所以A是可逆阵。 ,所以A是可逆阵。下面逐个求 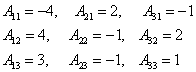
则  ,于是 ,于是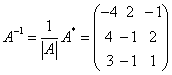
本题答案正确与否可通过 例3:设A为n阶方阵,证明: 证明:由 当 当 假设 |
三、逆矩阵的性质
|
例4:设A为n阶方阵,P为n阶可逆矩阵,试证:A为对称矩阵的充要条件是 证:(必要性) 设A为对称矩阵,即 设 由P与 |
|
例5:设n阶方阵A满足 解:由 于是: 由命题1, 又由: 于是 所以 例6:设A为3阶矩阵,且 解: 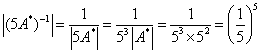
|
请认真答题,测试一下你对前面知识点的学习情况!
(单选题)7.若矩阵A可逆,则下列等式成立的是( )
【答案】C
【解析】
A.错误。应为![]() =
=![]() 。
。
B错误。应为![]()
C正确。![]()
【知识点】逆矩阵的性质
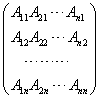 称为矩阵A的伴随矩阵,记为
称为矩阵A的伴随矩阵,记为