2.4 分块矩阵
一、分块矩阵的概念
把矩阵分块不仅可以带来运算上的方便,更对研究矩阵本身提供一种方法。 例如,设 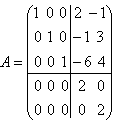
如上图,我们把它分成4小块,令 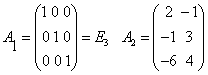 , ,则A的一个分块矩阵为 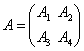 。 。
|
|
对任意一个 (1)A的行分块矩阵或A的行向量表示法: 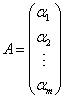 ,其中 ,其中(2)A的列分块矩阵或A的列向量表示法: 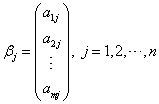
例如: 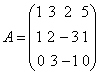
令 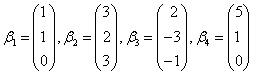 ,则A的按列分块矩阵为 ,则A的按列分块矩阵为 |
二、分块矩阵的运算
|
分块矩阵的运算仅是前面矩阵运算的换一种表达方法,并没有给出新的定义,只是把小块当作元素来进行运算。 例如分块矩阵的相加就是把相应的子块相加;分块矩阵的数乘就是用数去乘每个子块;分块矩阵的转置运算,就是把子块转置过去,当然也要把每个子块转置;分块矩阵的乘法也是把左矩阵的行与右矩阵的列对应相乘再相加后,作为乘积矩阵中的子块。 这里特别要注意:为保证子块相乘是可行的,在进行分块矩阵的乘法时,必须要求左矩阵的列分块方式与右矩阵的行分块方式一般。 |
|
例1:设 解:由分块矩阵加法, 从而 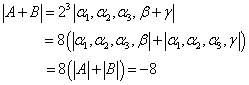
例2:设 解:转置矩阵是: 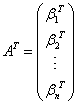
例3:设A为 解:AB为 若把A按行分块为 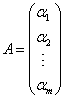 ,则 ,则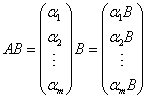 。 。特别 |
三、特殊分块矩阵求逆
分块对角矩阵有以下性质: (1) (2)A可逆 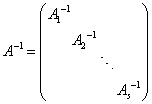
例4:设A,B均为可逆矩阵,证明: 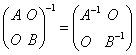 , ,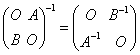
证明:由分块矩阵乘法 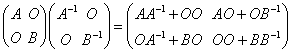
所以 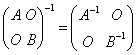
又 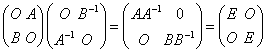
所以 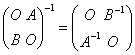
|
 的分块矩阵称为
的分块矩阵称为