5.1 特征值与特征向量
一、特征值与特征向量
注:①定义说明特征值与特征向量是紧密相连的概念,对每个特征值必有属于它的特征向量,且有无穷多个;而对每个特征向量必属于某个特征值,且只属于一个特征值。 ②特征向量必须是非零向量,且必是列向量。 ③若 因 |
我们看一下A的特征多项式: 设 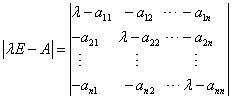
由行列式计算可知,行列式 |
|
下面我们从定义出发来推导求特征值、特征向量的方法: 1、写出并计算A的特征多项式 2、求特征方程 3、对于A的每一个特征值 |
|
例1:设 解:A的特征多项式 则A的两个特征值为 对 由此可求出方程组一个基础解系为 由此可求出方程组的一个基础解系为 |
|
例2:求 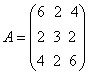 的特征值和线性无关的特征向量。 的特征值和线性无关的特征向量。解:A的特征多项式 
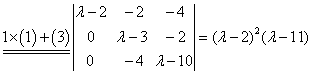
因此A的特征值为 对 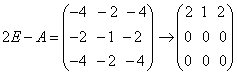
于是方程组的一般解为 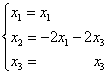 ,得一个基础解系为 ,得一个基础解系为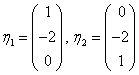 ,即为A的属于 ,即为A的属于对 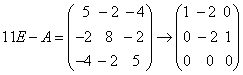
于是方程组的一般解为 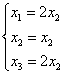 ,得一个基础解系为 ,得一个基础解系为 ,即为A的属于 ,即为A的属于 |
|
例3:证明:三角矩阵的特征值就是它的全体对角元。 证:不妨设A为n阶上三角矩阵 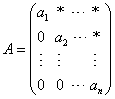
则A的特征多项式为 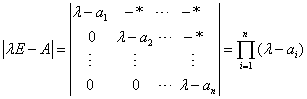
它的n个根就是A的n个对角元,即为A的n个特征值。 |
|
对于抽象的矩阵A,或由定义,或由求特征值的方法可以求出A的特征值和特征向量。 例4:设已知 (1) (2) (3)设 证:(1)用归纳法,当 于是对于任何自然数 (2)由 (3)设 于是 则有 说明:本例的结论很重要,希望能记住,特别是(3)给出了求多项式方阵的特征值的一个简便计算方法。只要 |
|
例5:设 解:由A是二阶上三角矩阵,其两个特征值为对角元1和3,而 所以B的两个特征值就是 |
|
例6:求出以下特殊的n阶方阵A的所有可能的特征值(m为某个正整数): (1) (2) 解:设 (1)由 (2)由 注:本例说明幂零矩阵的特征值必为0,对合矩阵的特征值必为 |
|
例7:若方阵A满足 解:当 当 |
二、关于特征值和特征向量的若干结论
|
命题1:实方阵的特征值未必是实数,特征向量也未必是实向量。 例8:求 解:由A的特征多项式 则A的两个特征值为 |
|
命题2:一个向量 证:设有 命题3:n阶方阵A和它的转置矩阵 证:由 说明A与 命题4:设 证:我们仅以二阶方阵对本命题说明:设 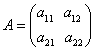 ,则A的特征方程为 ,则A的特征方程为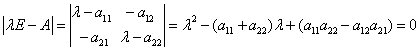 ,又因 ,又因也就有 比较两个方程的系数,即得 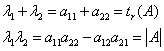
|
|
我们再以例2为例,三阶方阵A的三个特征值是 例9:已知三阶方阵A的特征值为 解:记 由A的特征值为 |
|
命题5:n阶矩阵A可逆 证:A可逆 设 因 |
请认真答题,测试一下你对前面知识点的学习情况!
(单选题) 21.设矩阵 ,则A的特征值为( )
,则A的特征值为( )
【答案】B
【解析】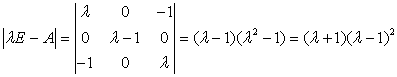 故A的特征值为
故A的特征值为
-1,1,1。
【知识点】特征值与特征向量