6.2 正定二次型和正定矩阵
一、实二次型的分类
| 对于任一个n元实二次型
|
|
例1:以n=3为例 (1)正定二次型: (2)半正定二次型: 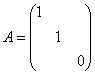 ; ;(3)负定二次型: (4)半负定二次型: 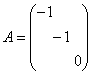
(5)不定二次型: 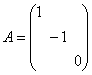
注意:(1)要讨论矩阵的正定性,该矩阵必须是实对称矩阵,二次型的正定性与实对称矩阵的正定性是紧密相连的。 (2)定义中要求X是任何非零向量,是指X的分量不全为零,即至少有一个分量不为零,而不是指所有分量全不为零的向量,因此如果仅对所有分量都不为零的向量X有 (3)二次型“正定”的含意就是指在任何非零向量X条件下,二次型 本课程中,只讨论正定二次型和正定矩阵,其它的统称为非正定二次型和非正定矩阵。 |
二、正定矩阵
|
首先介绍四个关于正定矩阵的定理:
证:设 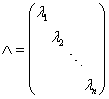
充分性:如果所有 必要性:设 于是对任意取定的 |
证:对任意取定的 由A的正定性必有: 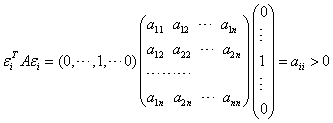
证毕 例2:问 解: 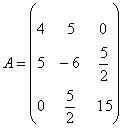 ,A中元素 ,A中元素 |
证:由A与B合同,即存在可逆矩阵P,使 如果A为正定矩阵,那么对于任何 反之,当B为正定矩阵时,由合同关系的对称性,A也是B的合同矩阵,则A也是正定矩阵。证毕 这个定理可以简述为:“正定矩阵的合同矩阵一定也是正定矩阵”或改用二次型语言:即二次型的正定性经可逆线性变换保持不变。
证:设A,B是两个同阶正定矩阵, 首先 注:这里 |
|
对于给定的对称矩阵,如何判定它的正定性?
证:由A为n阶实对称矩阵,故存在正交矩阵P,使 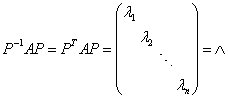 ,说明A与对角矩阵 ,说明A与对角矩阵则A正定 证毕。 推论(1)n阶对称矩阵A是正定矩阵 (2)n阶对称矩阵A是正定矩阵 (3)任意两个同阶正定矩阵必是合同矩阵。 证:(1)因为A的正惯性指数就是A的正特征值的个数。 所以A正定 (2)由对称矩阵的惯性定理,对任意一个n阶对称矩阵A,它一定合同于对角矩阵 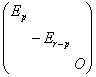 ,这里 ,这里由A正定 (3)设A和B都是n阶正定矩阵,则A与B都合同于n阶单位矩阵,则由合同关系的传递性,说明A和B都是合同矩阵。 |
|
在例3的证明过程中,已知正定矩阵A的行列式
显然一阶顺序主子式为 |
|
|
例4:判定 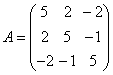 是不是正定矩阵? 是不是正定矩阵?解:A为实对称矩阵 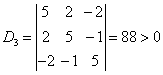
所在,A是正定矩阵。 例5:问 解: 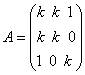 ,显然2阶顺序子式为 ,显然2阶顺序子式为所以 |
|
例6:问 (1) (2) 解:(1)  是对角矩阵。 是对角矩阵。而A正定当且仅当 (2) 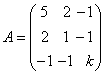
因 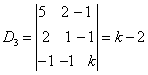
所以 |
请认真答题,测试一下你对前面知识点的学习情况!
(单选题) 25.若实对称矩阵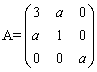 为正定矩阵,则a的取值应满足( ).
为正定矩阵,则a的取值应满足( ).
【答案】 B
【解析】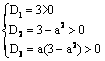
【知识点】正定矩阵
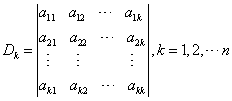 ,称为
,称为